| (1) |
Anne C. Hanna
ahanna@uiuc.edu
January 11, 2005
| (1) |
| (2) |
| (3) |
| (4) |
From the formula for the magnetic force on a single moving charge, the formula for the force on a current may be determined. If we have a segment of wire of length ![]() carrying a current
carrying a current ![]() flowing in a direction
flowing in a direction ![]() through a region of magnetic field
through a region of magnetic field ![]() , then the force on that tiny wire segment is
, then the force on that tiny wire segment is
| (5) |
For a long straight wire of length ![]() in direction
in direction ![]() , the total force on the wire is
, the total force on the wire is
| (6) |
| (7) |
A short wire segment of length ![]() carrying current
carrying current ![]() in a direction
in a direction ![]() creats a magnetic field at a point
creats a magnetic field at a point ![]() a distance
a distance ![]() from it equal to:
from it equal to:
| (8) |
A specific example of the use of this equation is the magnetic field of a wire loop oriented in the ![]() plane and centered at the origin. The above formula can be used to (relatively) easily compute the magnetic field anywhere on the
plane and centered at the origin. The above formula can be used to (relatively) easily compute the magnetic field anywhere on the ![]() -axis. If the loop has radius
-axis. If the loop has radius ![]() and current
and current ![]() , then the field at a distance
, then the field at a distance ![]() from the origin is:
from the origin is:
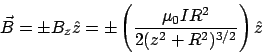 |
(9) |
The field off the ![]() -axis is much harder to find!
-axis is much harder to find!
| (10) |
| (11) |
The computation of ![]() can be a little tricky, but here's some possible distributions. For a long straight wire with current
can be a little tricky, but here's some possible distributions. For a long straight wire with current ![]()
| (12) |
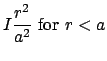 |
(13) | ||
| (14) |
| (15) | |||
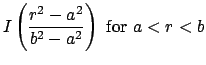 |
(16) | ||
| (17) |
| (18) | |||
| (19) |
If the sheet is oriented in the ![]() plane, with the current flowing in the
plane, with the current flowing in the ![]() direction, has
direction, has ![]() wires per unit length, and each wire carries a current
wires per unit length, and each wire carries a current ![]() , then the total magnetic field at any point is:
, then the total magnetic field at any point is:
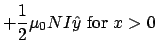 |
(20) | ||
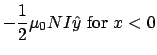 |
(21) |
| (22) |
| (23) |
| (24) |
A magnetic dipole with moment ![]() experiences a no net magnetic force when placed in an external magnetic field, but it will experience a torque (rotational force, units are Joules) due to the external field:
experiences a no net magnetic force when placed in an external magnetic field, but it will experience a torque (rotational force, units are Joules) due to the external field:
| (25) |
Finally, a magnetic dipole with moment ![]() in an external magnetic field
in an external magnetic field ![]() will have a magnetic potential energy equal to:
will have a magnetic potential energy equal to:
| (26) |
Recall that a potential energy maximum is an unstable equilibrium, that is, if the loop is nudged a little it will continue to rotate further away from the original orientation. A potential energy minimum is a stable equilibrium -- when slightly nudged it will return to its original position. For magnetic moment problems, ![]() is neither the maximum nor minimum value of the potential, and so is not an equilibrium point.
is neither the maximum nor minimum value of the potential, and so is not an equilibrium point.
| (27) |
Since a solenoid has a constant magnetic field inside it, related to its current by ![]() , if the solenoid has length
, if the solenoid has length ![]() and radius
and radius ![]() , and
, and ![]() turns per unit length, then the total stored energy in the solenoid when it carries current
turns per unit length, then the total stored energy in the solenoid when it carries current ![]() is:
is:
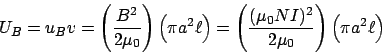 |
(28) |
| (29) |
| (30) |
The potential difference across an inductor, as a circuit element, is
| (31) |
| (32) |
Two inductors in parallel must have the same voltage difference across them, ![]() , and they may be replaced with an equivalent inductor whose inductance is
, and they may be replaced with an equivalent inductor whose inductance is
| (33) |
| (34) |
| (35) |
Note that the stored energy in an inductor (solenoid) is also related to the magnetic field inside it, as discussed in the section on magnetic field.
Specifically, Faraday's law states that a changing magnetic field generates an EMF around a closed wire loop based on the magnetic flux passing through said loop. If the loop has an area ![]() , then recall that the magnetic flux through the loop at a particular time
, then recall that the magnetic flux through the loop at a particular time ![]() is
is
![]() . Then the EMF which drives a current to flow around the loop will be:
. Then the EMF which drives a current to flow around the loop will be:
| (36) |
If the area of the loop is constant and the plane of the loop is perpendicular to the (varying) magnetic field, then:
| (37) |
The current which flows in the loop will be:
| (38) |
The sign convention for this equation is a little painful to contemplate. But the trick to remember is that the EMF (and the induced current flow) will circulate around the loop in such a direction that magnetic field generated by the induced current exactly opposes the change in the external magnetic field. If the external magnetic field points in the positive ![]() direction and its magnitude is decreasing then the induced current and EMF will circulate so as to create an induced magnetic field also pointing in the
direction and its magnitude is decreasing then the induced current and EMF will circulate so as to create an induced magnetic field also pointing in the ![]() direction.
direction.
Another way to compute the circulation direction for the EMF and current is to actually carefully work through the signs in the Faraday's law equation. You have to start by picking a direction for the area vector, so let's assume for simplicity's sake that the loop is in the ![]() plane. In this case, the area vector points either in the
plane. In this case, the area vector points either in the ![]() or
or ![]() direction. As viewed from the
direction. As viewed from the ![]() side, an area vector in the
side, an area vector in the ![]() direction indicates that the current and EMF circulate counterclockwise, while an area vector in the
direction indicates that the current and EMF circulate counterclockwise, while an area vector in the ![]() direction indicates that the current and EMF circulate clockwise. But since we don't initially know the circulation direction of the current, we cannot be sure which of these directions for the area vector will be correct. All you can really do is pick one and be consistent. If the direction you have chosen is opposite the actual direction, then you will discover that your computed values for the EMF and current are negative (but the magnitudes will still be correct).
direction indicates that the current and EMF circulate clockwise. But since we don't initially know the circulation direction of the current, we cannot be sure which of these directions for the area vector will be correct. All you can really do is pick one and be consistent. If the direction you have chosen is opposite the actual direction, then you will discover that your computed values for the EMF and current are negative (but the magnitudes will still be correct).
This method requires extreme care with the signs. You may pick up minus signs from the
![]() dot product and from the
dot product and from the ![]() time derivative, and there will always be a minus sign in the definition of the EMF,
time derivative, and there will always be a minus sign in the definition of the EMF,
![]() , due to Lenz' law.
, due to Lenz' law.
Once a current flows in the loop, it can experience a torque due to the external magnetic field as described above. (The induced magnetic field is usually neglected in this computation, since it causes no net torque on the loop.) It will also have a magnetic potential energy due to the external magnetic field.
| (39) |
You may have a loop of constant area moving from a region of zero magnetic field into a region of constant magnetic field. In this case, the flux through the loop is constant as long as it is completely outside or completely inside the field region, so there is no EMF and no current in either of these cases. The loop will only experience an EMF as it is entering or leaving the magnetic field region, and the EMF will then be:
| (40) |
Finally, you may have a loop of constant area in a region of constant magnetic field, where the loop rotates on a pivot (usually one of its edges). Then the loop area and the magnetic field are constant, but their relative direction changes. So when the loop's area vector makes an angle ![]() with the magnetic field, then the magnetic flux through the loop is:
with the magnetic field, then the magnetic flux through the loop is:
| (41) |
| (42) |
| (43) |
There is one final problem, which I don't know if you'll get or not, where the magnetic field is constant, but the loop area is changing (eg. one side is a bar sitting on metal rails, moving along the rails). For this case the EMF is:
| (44) |
If the inductor is simply in a circuit with a battery, theoretically the current through the inductor will simply increase at a constant rate until all the energy stored in the battery has been transferred to the inductor (and the voltage difference across both is zero, because the battery has no energy and the current through the inductor is constant). So usually, we put a resistor in series with the inductor, thus limiting the maximum current flow through the inductor.
The theory in this case is that we let the circuit evolve over time until it reaches a steady state. In the steady state, the current through the inductor is constant and so ![]() (although
(although ![]() may or may not be zero), and the voltage across the inductor is also zero. (It acts like a wire.) So if we simply put a resistor in series with the inductor, in the steady state all of the battery voltage will be across the resistor, and the current through the resistor (and inductor) will simply be
may or may not be zero), and the voltage across the inductor is also zero. (It acts like a wire.) So if we simply put a resistor in series with the inductor, in the steady state all of the battery voltage will be across the resistor, and the current through the resistor (and inductor) will simply be
![]() .
.
As the inductor is charging up to this maximum current, we can compute the current through it at any time using a formula similar to that for a charging capacitor:
| (45) |
| (46) |
When we take the battery out of the circuit and discharge the inductor, the current through the inductor will vary as:
| (47) |
Just as a changing magnetic field creates an electric field (Faraday's law), a changing electric field can also create a magnetic field, as if there was a current flowing nearby. This imaginary current is called the ``displacement current''. If you want to find the induced magnetic field at a given point ![]() due to a changing electric field then these are the steps you follow:
due to a changing electric field then these are the steps you follow:
First draw an Ampèrian loop which passes through ![]() , is perpendicular to the change in the electric field, and shares the symmetry of the charge/current distribution.
, is perpendicular to the change in the electric field, and shares the symmetry of the charge/current distribution.
Next, compute the electric flux passing through the Gaussian surface enclosed by that loop, using Gauss' law, as a function of time.
The displacement current is defined as:
| (48) |
This current will be the total piercing current for your Ampèrian loop, and it will flow in the direction of the change in the electrical field. You can then use it to compute the magnetic field via Ampère's law.
The canonical example is a charging parallel-plate capacitor with circular plates. The plates each have radius ![]() , and a current
, and a current ![]() is going into the left plate and out of the right one. So the charge on the left plate at any given time is
is going into the left plate and out of the right one. So the charge on the left plate at any given time is ![]() , where
, where
![]() . The right plate, of course, has a charge of
. The right plate, of course, has a charge of ![]() . The electric field between them can be approximated by treating the capacitor plates as infinite parallel plates, so
. The electric field between them can be approximated by treating the capacitor plates as infinite parallel plates, so
![]() .
.
We want to find the induced magnetic field at a distance ![]() from the center axis of the plates. So we draw an Ampèrian loop of radius
from the center axis of the plates. So we draw an Ampèrian loop of radius ![]() aligned in the
aligned in the ![]() plane and centered along the plate axis (the
plane and centered along the plate axis (the ![]() -axis). The Gaussian surface defined by this Ampèrian loop is a disk of radius
-axis). The Gaussian surface defined by this Ampèrian loop is a disk of radius ![]() , also centered at the plate axis. So the electric flux through this Gaussian surface is
, also centered at the plate axis. So the electric flux through this Gaussian surface is
![]() . Thus the displacement current is
. Thus the displacement current is
![]() . Since the electric field is increasing in magnitude and pointing right, the displacement current also flows right.
. Since the electric field is increasing in magnitude and pointing right, the displacement current also flows right.
So the magnetic field at a radius ![]() from the center of the plates is simply that of a current
from the center of the plates is simply that of a current ![]() flowing to the right along the
flowing to the right along the ![]() axis. It will therefore satisfy Ampère's law:
axis. It will therefore satisfy Ampère's law:
![]() , where the loop has radius
, where the loop has radius ![]() and the magnetic field is parallel to the loop at every point. Thus the magnetic field is:
and the magnetic field is parallel to the loop at every point. Thus the magnetic field is:
| (49) |
This document was generated using the LaTeX2HTML translator Version 2002-1 (1.68)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split=0 exam2notes.tex
The translation was initiated by Anne C. Hanna on 2005-01-11