Anne C. Hanna
ahanna@uiuc.edu
January 11, 2005
| (1) |
| (2) |
Note that the ![]() ,
, ![]() , and
, and ![]() components of the electric force on
components of the electric force on ![]() are:
are:
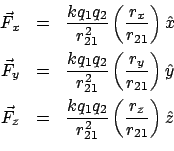
If we have several point charges (or several charged insulating objects) and we want to find the net electric field due to these objects at a particular point ![]() , then we use the superpostion principle. Each individual object, in isolation, would create a field
, then we use the superpostion principle. Each individual object, in isolation, would create a field
![]() , (where
, (where
![]() is the distance vector from the object to the point
is the distance vector from the object to the point ![]() ) and the total field is just the sum of all these individual fields:
) and the total field is just the sum of all these individual fields:
| (3) |
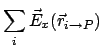 |
(4) | ||
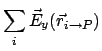 |
(5) | ||
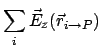 |
(6) |
| (7) |
| (8) |
Gauss' law allows the computation of the electric field in certain symmetrical situations. In each case, the procedure begins with drawing a Gaussian surface which passes through the point where you want to find the electric field and which shares the symmetry of the charge distribution. Then we compute the flux through this surface in two different ways: using the definition of flux, and using Gauss' law. If we have chosen our Gaussian surface well, the electric field will have constant magnitude on and be perpendicular to certain parts of the surface (the parts where we want to know the electric field, which have total area
![]() ), and will be zero on or tangent to the rest of the surface (the parts where we don't care about the field, which have total area
), and will be zero on or tangent to the rest of the surface (the parts where we don't care about the field, which have total area
![]() ). Then the definition of flux tells us that
). Then the definition of flux tells us that
![]() , since the surface has been designed so that the flux through the other regions is zero. Next we count the total enclosed charge inside the surface,
, since the surface has been designed so that the flux through the other regions is zero. Next we count the total enclosed charge inside the surface,
![]() , which, using Gauss' law, gives:
, which, using Gauss' law, gives:
![]() . We can then equate these two formulae for the flux and solve for the electric field at the point in question:
. We can then equate these two formulae for the flux and solve for the electric field at the point in question:
| (9) |
Below we discuss the computation of
![]() and
and
![]() for the various possible symmetries.
for the various possible symmetries.
| (10) |
For a point charge ![]() , the enclosed charge at any radius is simply:
, the enclosed charge at any radius is simply:
| (11) |
The total charge in a solid insulating sphere of radius ![]() and volume charge density
and volume charge density
![]() is:
is:
| (12) |
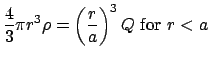 |
(13) | ||
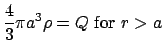 |
(14) |
For a thin hollow spherical insulating shell of radius ![]() with an area (or ``surface'') charge density
with an area (or ``surface'') charge density
![]() (or for the inner or outer surface of a metal sphere) the total charge is:
(or for the inner or outer surface of a metal sphere) the total charge is:
| (15) |
| (16) | |||
| (17) |
For a hollowed insulating sphere with inner radius ![]() , outer radius
, outer radius ![]() , and volume charge density
, and volume charge density
![]() the total charge is:
the total charge is:
| (18) |
| (19) | |||
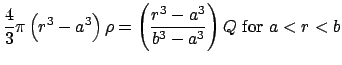 |
(20) | ||
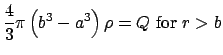 |
(21) |
For any spherically symmetric charge distribution, Gauss' law tells us that the electric field at a radius ![]() from the center is simply:
from the center is simply:
| (22) |
where
![]() is the total charge within a radius
is the total charge within a radius ![]() of the center.
of the center.
Note that if we have a metal sphere of radius ![]() with an air pocket in the center of radius
with an air pocket in the center of radius ![]() , then the electric field in the actual metal will be zero, so in order to ensure this, the surface charge on the inner surface of the sphere will be equal to the negative of the total charge
, then the electric field in the actual metal will be zero, so in order to ensure this, the surface charge on the inner surface of the sphere will be equal to the negative of the total charge ![]() trapped inside the air pocket. (Then Gauss' law says that
trapped inside the air pocket. (Then Gauss' law says that
![]() for
for ![]() .) Whatever charge is leftover goes to the outer surface. So if the sphere has a net charge
.) Whatever charge is leftover goes to the outer surface. So if the sphere has a net charge ![]() , then the outer surface will have a total charge
, then the outer surface will have a total charge ![]() . So, if the trapped charge is a a point charge
. So, if the trapped charge is a a point charge ![]() at the center of the sphere then the electric field at a radius
at the center of the sphere then the electric field at a radius ![]() will be:
will be:
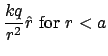 |
(23) | ||
| (24) | |||
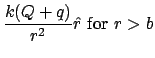 |
(25) |
| (26) |
| (27) |
In particular, a thin charged wire will simply be described as having a charge per unit length ![]() , so that
, so that
| (28) |
For a solid insulating cylinder with radius ![]() and volume charge density
and volume charge density
![]() the charge per unit length is:
the charge per unit length is:
| (29) |
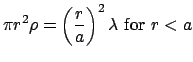 |
(30) | ||
| (31) |
A thin cylindrical insulating shell of radius ![]() (or the inner or outer surface of a cylindrical piece of metal) with area (``surface'') charge density
(or the inner or outer surface of a cylindrical piece of metal) with area (``surface'') charge density
![]() has a charge per unit length:
has a charge per unit length:
| (32) |
| (33) | |||
| (34) |
For a solid insulating cylinder with its center cut out, inner radius ![]() , outer radius
, outer radius ![]() , and volume charge density
, and volume charge density
![]() the total charge per unit length is:
the total charge per unit length is:
| (35) |
| (36) | |||
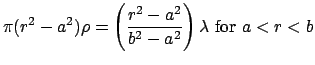 |
(37) | ||
| (38) |
For such a charge distribution, Gauss' law gives the electric field at a distance ![]() from the axis to be:
from the axis to be:
| (39) |
where
![]() is the total charge per unit length within a distance
is the total charge per unit length within a distance ![]() of the axis.
of the axis.
For a solid metal cylinder with charges trapped in an air pocket in the center, the charges on its inner and outer surfaces are similar to those for the spherical case.
| (40) |
The enclosed charge inside this Gaussian pillbox will be:
| (41) |
For a thin insulating sheet or a single surface of a metal slab, the charge per unit area is simply given as the surface charge density ![]() .
.
The total charge per unit area on a metal slab is the sum of the surface charges on both sides of it:
| (42) |
For a solid insulating slab of thickness ![]() with charge per unit volume
with charge per unit volume ![]() , the charge per unit area is:
, the charge per unit area is:
| (43) |
So from Gauss' law, the electric field anywhere outside a single uniformly charged sheet or slab oriented in the ![]() plane is:
plane is:
| (44) |
For a collection of charged sheets or slabs, the electric field is:
| (45) |
If
![]() then the field points to the right, and if
then the field points to the right, and if
![]() then the field points left. (eg.
then the field points left. (eg.
![]() ,
,
![]()
![]() )
)
Note that the field inside a metal slab is always 0, and we can use this fact to find the charges on its two surfaces, ![]() and
and ![]() . Since we have two unknown quantities, we need two equations in order to solve for them. First of all, we are usually given that the total charge per unit area on the slab is
. Since we have two unknown quantities, we need two equations in order to solve for them. First of all, we are usually given that the total charge per unit area on the slab is ![]() , and this must be equal to the sum of the two surface charges:
, and this must be equal to the sum of the two surface charges:
| (46) |
| (47) |
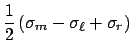 |
(48) | ||
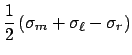 |
(49) |
The following equation shows how to compute the amount by which the potential increases when you go from point ![]() to point
to point ![]() . It's equal to the work done when you carry a charge
. It's equal to the work done when you carry a charge ![]() from point
from point ![]() to point
to point ![]() , divided by
, divided by ![]() , and it's also equal to the negative integral of the electric field along any path from
, and it's also equal to the negative integral of the electric field along any path from ![]() to
to ![]() (since the electric force is conservative).
(since the electric force is conservative).
Conversely, the electric field associated with a given electric potential ![]() is:
is:
| (51) |
| (52) |
If the source of the potential is a point charge ![]() at the origin:
at the origin:
| (53) |
If the source of the potential is a thin, infinitely-long wire with charge per unit length ![]() :
:
| (54) |
If ![]() and
and ![]() are both points within the same chunk of conductor:
are both points within the same chunk of conductor:
| (55) |
Also note that the electric potential is continuous everywhere (its value doesn't have sudden jumps), and the potential is constant (although not necessarily zero) everywhere inside a conductor. (Don't forget that the wires in an electrical circuit are conductors!)
For a single point charge located at the origin:
| (56) |
where ![]() is the electric potential at infinity.
is the electric potential at infinity.
For a collection of point charges ![]() at distances
at distances ![]() from the point where the potential is desired:
from the point where the potential is desired:
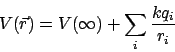 |
(57) |
So if you need to find the sign of a potential difference ![]() , then check the above conditions. If
, then check the above conditions. If ![]() the potential difference will be positive. If you need to find the sign of an absolute potential
the potential difference will be positive. If you need to find the sign of an absolute potential ![]() , then you need to look at the reference point where
, then you need to look at the reference point where ![]() . If a positive charge is happier at the reference point then
. If a positive charge is happier at the reference point then ![]() ; if a positive charge is less happy at the reference point then
; if a positive charge is less happy at the reference point then ![]() .
.
(Note that negative charges are actually happier at higher potentials.)
The next step is to choose a path between the two points. Since the electric force is conservative, in principle any path between them whatsoever will do, but in practice some paths are easier to compute than others. For circuits, the path should of course be along one of the wire tracks. In this case the electric potential will be constant along the wires and will increase or decrease only when crossing from one side to the other of a circuit element. For other arrangements a path composed of segments parallel to or perpendicular to the electric field is generally the simplest route to take. In this case, the potential will be constant on the perpendicular segments and will vary continuously along the parallel segments. Note also that the potential may vary differently in different regions, depending on what the electric field is in each region. (For example, it will be constant inside a conductor, since the electric field is zero there.)
Finally, you are ready to integrate along the path. Starting at point ![]() or the reference point, write down the potential there (using the assumptions discussed above). Now look at the first segment of the path. Integrate the electric field along this path segment, according to the defining equation (50) for electrical potential. (Note that if the electric field varies at all along the segment then it is not appropriate to just multiply the electric field at some point on the segment by the segment's length. This will almost always give you the wrong answer.) For electric circuit elements, the magnitude of the potential difference will just be the potential
or the reference point, write down the potential there (using the assumptions discussed above). Now look at the first segment of the path. Integrate the electric field along this path segment, according to the defining equation (50) for electrical potential. (Note that if the electric field varies at all along the segment then it is not appropriate to just multiply the electric field at some point on the segment by the segment's length. This will almost always give you the wrong answer.) For electric circuit elements, the magnitude of the potential difference will just be the potential ![]() across the circuit element, for example
across the circuit element, for example ![]() for a battery.
for a battery.
Then determine if the potential increases or decreases along this path segment (moving from ![]() or
or ![]() towards
towards ![]() or
or ![]() , respectively), using the sign criteria above. Don't forget that an electrical current is a flow of positive charges, so the direction of current flow in a circuit tells you about the sign of potential differences. If the potential increases along the path segment, then you should add the potential change to the starting potential. If it decreases, then you should subtract the change from the starting potential.
, respectively), using the sign criteria above. Don't forget that an electrical current is a flow of positive charges, so the direction of current flow in a circuit tells you about the sign of potential differences. If the potential increases along the path segment, then you should add the potential change to the starting potential. If it decreases, then you should subtract the change from the starting potential.
Repeat this process along each segment until you reach the endpoint (![]() or
or ![]() ) of the path and you'll have your answer.
) of the path and you'll have your answer.
| (58) |
Another way to think of electric potential is to imagine that we have one completely isolated charge, ![]() , in a region of no electric field. If we release this charge, it will not go anywhere at all, so we can think of it as having no electric potential energy. Now we bring in a second charge,
, in a region of no electric field. If we release this charge, it will not go anywhere at all, so we can think of it as having no electric potential energy. Now we bring in a second charge, ![]() and place it at a distance
and place it at a distance ![]() from
from ![]() . If we hold
. If we hold ![]() fixed and release
fixed and release ![]() ,
, ![]() will either fly off to infinity or fall towards
will either fly off to infinity or fall towards ![]() , depending on their relative signs. The kinetic energy it gains as it flies off to infinity, or the kinetic energy it could have gained by falling from infinity to
, depending on their relative signs. The kinetic energy it gains as it flies off to infinity, or the kinetic energy it could have gained by falling from infinity to ![]() , is due to a change in its electric potential energy with respect to the situation where it was isolated. So we can write that the electric potential energy stored in the arrangement of a pair of charges,
, is due to a change in its electric potential energy with respect to the situation where it was isolated. So we can write that the electric potential energy stored in the arrangement of a pair of charges, ![]() and
and ![]() , separated by a distance
, separated by a distance ![]() is:
is:
| (59) |
In general, if we have two or more charges, then the potential energy is:
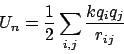 |
(60) |
The change in potential energy when a charge is moved from point ![]() to point
to point ![]() is equal to the work done in moving the charge between those two points. If the potential energy increases then you must do positive work on the charge to push it up the potential hill. If the potential energy decreases, then one would have to do negative work on the charge. In other words, you can actually use the charge's motion down the potential hill to do work on another object.
is equal to the work done in moving the charge between those two points. If the potential energy increases then you must do positive work on the charge to push it up the potential hill. If the potential energy decreases, then one would have to do negative work on the charge. In other words, you can actually use the charge's motion down the potential hill to do work on another object.
| (61) |
The total stored energy in a capacitor when it's charged up to a charge ![]() is:
is:
| (62) |
The power dissipated in a capacitor is:
| (63) |
| (64) |
The total capacitance of two capacitors in series is:
| (65) |
| (66) |
The following gives the capacitance of a concentric spherical capacitor filled with vacuum or air, where the radius of the inner spherical conductor is ![]() while the outer spherical conductor has radius
while the outer spherical conductor has radius ![]() .
.
| (67) |
The capacitance of a concentric cylindrical capacitor of length ![]() filled with vacuum or air, where the inner conductor has radius
filled with vacuum or air, where the inner conductor has radius ![]() and the outer conductor has radius
and the outer conductor has radius ![]() , is:
, is:
| (68) |
| (69) |
| (70) |
Note that if you have a parallel plate capacitor with plate separation ![]() and area
and area ![]() and you insert a dielectric with thickness
and you insert a dielectric with thickness ![]() and area
and area ![]() then this capacitor can be treated as two capacitors in series:
then this capacitor can be treated as two capacitors in series:
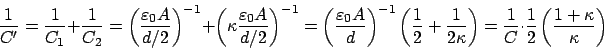
| (71) |
| (72) |
| (73) |
Note that the final voltage across the capacitor is not necessarily equal to the voltage across the battery. In particular
![]() if there is a resistor in parallel with the capacitor and another resistor in series with the resistor-capacitor combination.
if there is a resistor in parallel with the capacitor and another resistor in series with the resistor-capacitor combination.
When a capacitor is discharging, the charge on the capacitor varies over time as:
| (74) |
| (75) |
The instantaneous power dissipated by a resistor is:
| (76) |
The energy stored in a resistor is:
| (77) |
| (78) |
Two resistors in parallel have an equivalent resistance:
| (79) |
The resistance of a chunk of material of length ![]() and cross-sectional area
and cross-sectional area ![]() (that is, the current travels a distance
(that is, the current travels a distance ![]() in crossing the chunk, and the current flow has a cross-section
in crossing the chunk, and the current flow has a cross-section ![]() ) is:
) is:
| (80) |
This document was generated using the LaTeX2HTML translator Version 2002-1 (1.68)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split=0 exam1notes.tex
The translation was initiated by Anne C. Hanna on 2005-01-11