Fair Surface Design

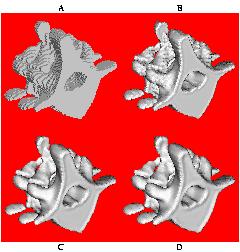
This project is based on Taubin's Fair Surface Design algorithm, which uses a non-shrinking variant of the Gaussian smoothing algorithm to move vertices in and out in order to smooth a polygon mesh. The image above is (frame A) from a CT scan of a spine, and frames B, C, and D are successively more smoothed versions thereof. The goal of the project was to build an Open Inventor based tool for smoothing meshes, allowing constraints to be set and subdivision to be done. The final product allows fairing using arbitrary sequences of Gaussian parameters, mesh subdivision, setting of hierarchical constraints and fixed points, arbitrary motion of mesh points, and motion of mesh points with smooth deformation.

Contents:

• The underlying theory
• My planned implementation timeline
• Implementation journal
• Download the final code
• Papers referenced

All images on this page (besides the screen shots) are from 1 .

Theory

Algorithm

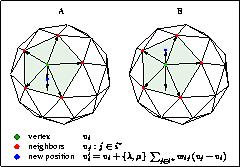
For each vertex on the mesh, calculate delta-x as the weighted sum of the vectors from the vertex to its neighbors. Then, for each vertex, add in lambda (where lambda is a number between 0 and 1) times delta-x. Then repeat the algorithm, but instead of lambda, use mu (where mu is a negative number, less than -lambda). Both steps are repeated in sequence several times, until the mesh is sufficiently smooth. Without the second step, this produces Gaussian smoothing, which causes shrinkage of the mesh over time. The second step counteracts the shrinkage while still smoothing the mesh.

1, sections 1 and 2

More Efficient Filters

2

Subdivision

By repeatedly subdividing the mesh (breaking each polygonal face into multiple, smaller faces) and then applying the smoothing algorithm, a rough approximation of a surface can be turned into a much prettier surface than smoothing or subdivision alone.

1, section 3

Constraints

Hierarchical Constraints

By manipulating the internal representation of the mesh, it is possible to have two vertices, x and y, such that x considers y to be its neighbor, but y does not consider x to be its neighbor. This is called a non-symmetric neighborhood structure. The effect of such a manipulation on the smoothing algorithm is that x will use y's position to calculate its new position, but y will be independent of x. If y has been completely isolated, i.e. some points consider y a neighbor, but y considers itself to have no neighbors, then y will remain fixed through successive iterations of the algorithm, while still affecting surrounding vertices. An example of this can be seen in frame C of the picture above: the vertices at the foot were defined as having empty neighborhoods, so they remained stationary through the smoothing algorithm.

1, section 4.1

As an extension of this idea, a weight l can be attached to each vertex. If two vertices x and y have weights lx and ly, and they would otherwise be considered neighbors of one another (for example, because they share an edge in the mesh), then x is a neighbor of y only in ly <= lx. For example, if you were to give a set of points a label which is higher than the label the other points have, those points would only take one another into consideration as the smoothing progresses, but would affect other points. You could thus build an infrastructure about which the rest of the smoothing must be done. This is useful when you want to preserve certain aspects of the original shape of the mesh which might otherwise be smoothed away by the algorithm. An example can be seen in frame D of the picture above: the vertices at the foot have been labeled in such a way that they move only under the influence of one another, but still affect outside points.

1, section 4.4

Smooth Deformations

1, sections 4.2 and 4.3

Timeline

• 4/15/97: build a tool to make example meshes by sudividing simpler meshes and jittering new coordinates in the direction of the centroid
• 4/28/97: build Inventor based tool that can do fairing of triangular meshes using Taubin's algorithm
• 5/5/97: add support for more efficient filters as discussed in the second paper
• 5/12/97: add ability to execute sequences of alternating subdivision and fairing
• 5/19/97: add ability to add hierarchical (neighborhood manipulation) constraints
• 6/2/97: add smooth interpolation (ability to move points and have shape smooth about it)

Implementation Blow by Blow, with Screen Shots

• 4/27/97: got preliminary fairing to work. These pictures represent a gaussian smoothing algorithm, with lambda=1.0, applied 0, 1, and 20 times. Because it's plain gaussian smoothing, every smoothing step makes the overall shape smaller, a fact that's hidden because they were automatically resized when I did the image capture.

  

• 5/3/97: added ability to read in a file containing a schedule of lambda and mu pairs to use in smoothing. This allows you to try out some of the more efficient combinations discussed in 2. With parameters chosen according to the rules, there is no shrinkage. The image below is the same mesh seen in the first image above, faired with the set of parameters described in 2, figure 9 part F (24 steps total). Note that it looks suspiciously like the image above after a single step of gaussian smoothing.

  

• 5/13/97: subdivision works. Oddly enough, a 64-face mesh shrinks rapidly when a normally stable lambda/mu schedule is applied to it, but if the same mesh is once subdivided, it starts to grow (slightly) when fairing. The picture shows a simple 64 face mesh, then the same mesh subdivided to 4096 faces (after which it looks the same) and then faired by 24 steps of the schedule from 2, figure 9-F, and then the original mesh, with four sequences consisting of six fairing and one subdivision applied (same schedule). Note that the last mesh shrank because it was only 64 faces when the first six fairing steps set in. I don't know why that has that effect, though.

  

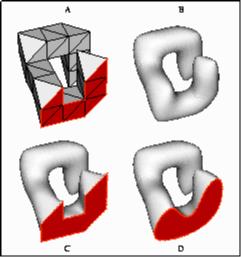
• 5/18/97: hierarchical constraints work now, despite some unidentified inventor problems. Shown here is the same old mesh you've seen so many times before, with the corner points fixed and thousands of fairing steps applied.

  

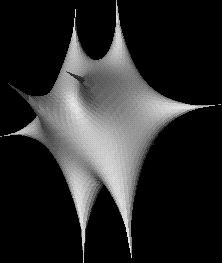
• 6/12/97: added fixed points, in addition to the hierarchical constraints. This allows you to actually make useful skeleton loops, since if you make a loop (set of vertices each of which is connected to two others) with a higher label than the surrounding points, they will shrink and take the rest of the mesh with it (higher connectivity skeletons -- not sure where the border is -- don't have this problem). Also added ability to move points, and (much cooler) smooth deformation: the ability to move points and have the surrounding points automatically smoothed in real time. I created the thing below by smoothing, subdividing, moving points, and smoothly deforming the original dodecahedral (or whatever it is) mesh.

  

• 6/12/97: (later the same day) realized that the scope of the smooth deformation can be changed by changing the number of times the delta signal is smoothed. Added ability to manipulate this from within the program.

Source code

• The completed project code tarball.
• The README from the project code tarball, half-assedly converted to HTML.
• The version of STL I used, in a tarball.

References

1. Taubin, G., "A Signal Processing Approach to Fair Surface Design," Computer Graphics Proceedings, pp. 351-358, August 1995.
2. Taubin, G., "Optimal Surface Smoothing as Filter Design," Research Report, March 1996.

author