Current is measured in units called amps or amperes or A. It is represented by the letter I in equations.
At 0V between two points, no electrons will move between those points. No current will flow if those points are connected by a wire. It's like putting a pipe between two ends of a flat lake: no water flows through the pipe.
A small voltage (like 1.5V from an AA battery) is like a fairly flat river. If you put a pipe (wire) between two points along the river, water will flow. But for a given size pipe, the amount of water per second won't be very big.
A high voltage (say, 120V) is like a waterfall along that river. If you put that same pipe between the top and the bottom of that waterfall, water will flow like crazy.
But voltage is not the same as capacity. Say you have a small stream flowing parallel to the river. If you put a small pipe from one point along each waterway to a set distance downstream, you will get the same amount of water flow in each of the two pipes. But if you replace the small water pipe with a big water pipe, the stream won't be able to provide enough water to fill the pipe, and you'll get more water in the river-pipe than the stream-pipe. The stream and the river result in the same drop in water pressure from one point to another (like a voltage), but can provide a different maximum amount of water (just like lower capacity batteries go dead earlier than high capacity batteries).
A battery is rated both with a voltage (like 1.5V) and a capacity (like 1600mAh). A dead battery has run out of charge - it has exhausted its store of electrons. It's like an empty water tower.
Voltage is measured in units called volts or V. It is represented by the letter V in equations.
Resistance is measured in units called Ohms or. It is represented by the letter R in equations.

| black | brown | red | orange | yellow | green | blue | violet | grey | white | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
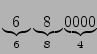 .
That's a lot of zeros to count, so people usually add prefixes to the
units to remove zeros in sets of three.
The most common prefixes are k for 3 zeros, and
M for 6 zeros.
So instead of 680000
.
That's a lot of zeros to count, so people usually add prefixes to the
units to remove zeros in sets of three.
The most common prefixes are k for 3 zeros, and
M for 6 zeros.
So instead of 680000
The fourth stripe that's a little further from the others indicates the
tolerance, or how precisely the resistor's value actually matches what
the color code indicates. So if you have a 100![]() resistor with a
5% tolerance, that resistor could actually be anywhere between
95
resistor with a
5% tolerance, that resistor could actually be anywhere between
95![]() to 105
to 105![]() . What the resistor companies actually do is
they fabricate lots of resistors, then measure them and sort them by
tolerance. So in practice, if a resistor has a 5% band on it, its
value will be between 95 and 97.99999
. What the resistor companies actually do is
they fabricate lots of resistors, then measure them and sort them by
tolerance. So in practice, if a resistor has a 5% band on it, its
value will be between 95 and 97.99999![]() or between 102.00001 and
105
or between 102.00001 and
105![]() . All the resistors between 98 and 102
. All the resistors between 98 and 102![]() will have
been labelled as 2% resistors by the manufacturer and sold at a higher
price. The colors for tolerance are:
will have
been labelled as 2% resistors by the manufacturer and sold at a higher
price. The colors for tolerance are:
| brown | red | gold | silver | none |
| 1% | 2% | 5% | 10% | 20% |
Batteries also differ in how many electrons they store - their capacity - measured in milliamp-hours (mAh). Voltage tells you how strongly the battery pressures the electrons to flow. Capacity tells you how many of those electrons it holds. The capacity of our batteries is about 1650mAh. This means that if we were to use the battery to power one LED, drawing 20mA of current, the battery would last over 80 hours.
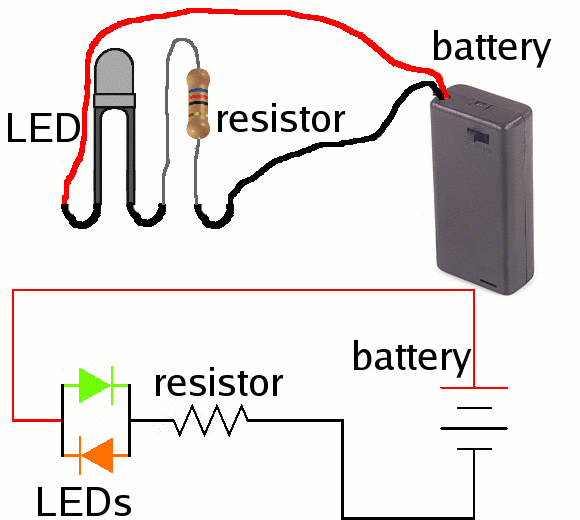
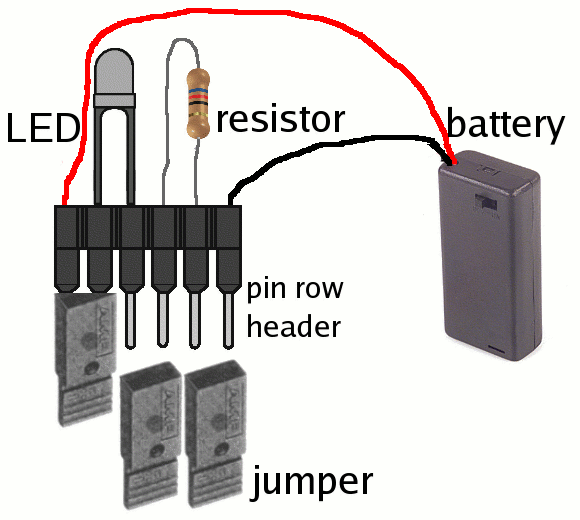
We will be using two batteries. There are a couple of ways to connect batteries shown in Fig. 2.2.
Connecting batteries in parallel is like putting two water towers next to each other. The water pressure would be the same as with a single battery (so the voltage doesn't change). But we have twice as much water (so we double the capacity). Connecting batteries in series is like stacking two water towers on top of each other, making a water tower that is twice as tall. We have twice as much water pressure (so the voltage is doubled).We will connect our batteries in series. The two 1.5V batteries will give us 3V.
The LED component we're using actually contains two LEDs. The red LED faces one way and the green LED faces the other way. So depending on how you connect it in the circuit, one or the other will glow but not both.
Let's do an example calculation.
What do we plug in for V, the voltage? The two batteries are 1.5V each.
We've connected them in series. It's like stacking one water tower on
top of another: the result is twice as high. So our two 1.5V
batteries are like one 3.0V battery. So use ![]() .
.
What do we plug in for R, the resistance? You have three resistors in your kit,
each with a different resistance. The colored stripes on the resistor
indicate the value of the resistor. One of those resistors
is 680![]() . So use
. So use ![]() . Note that the LED has some
resistance of its own. But the resistance of the LED is so low that
it gets dwarfed by the resistor, so we can ignore the LEDs resistance.
. Note that the LED has some
resistance of its own. But the resistance of the LED is so low that
it gets dwarfed by the resistor, so we can ignore the LEDs resistance.
What do we plug in for I, the current? Well, that's what we calculate! Ohm's Law will tell us how much current (I) to expect given the voltage (V) provided by the battery, and the resistance (R) from the resistor that we choose. It can help us pick the correct resistor. So let's do some math:
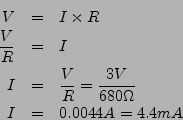
What do you think will happen if we put in a smaller resistor? Look
back at:
![]() . If we make R smaller, that's makes the
whole fraction bigger. Look at an example:
. If we make R smaller, that's makes the
whole fraction bigger. Look at an example:
| 
|